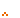*15分鐘延遲 *15 min. Delay Quote *15分钟延迟

	開市價 Open 开市价	最高價 High 最高价	最低價 Low 最低价	前收市價 LastClosePrice 前收市价	按盤價 Price 按盘价	升跌 Change 升跌
*延遲15分鐘報價 *Quotes are delayed for 15 minutes. *延迟15分钟报价

Futures Options Trading Details Contract Details Contract Money

Options

Definition | Types of Options | Pricing | Common Strategy: Single Strategy | Portfolio Strategy

Definition
Options contracts give buyers the right (not obligation) to buy / sell the underlying assets at a specific time and strike price. If the option is exercised, seller must have an obligation to fulfill the transaction. In short, options are classified into call options and put options.

 Types of Options 

1. Call Options
   Gives the buyer the right (not obligation) to buy the underlying assets at / before the specified time (depends whether it is a European or American option) at a strike price as specified in the contract. If the buyer chooses to enforce the right to exercise the option, the other party (seller) must have the obligation to sell the assets or pay the difference in cash value between the settlement price and the strike price.
2. Put Options
   Gives the buyer the right (not obligation) to sell the underlying assets at /before the specified time (depends whether it is a European or American option) at a strike price as specified in the contract. If the buyer chooses to enforce the right to exercise the option, the other party (seller) must have the obligation to buy the assets or pay the difference in cash value between the settlement price and the strike price.
3. Special Options
   Standardized options are usually traded on the Hong Kong Stock Exchange, and special options with non-standardized terms are traded in the OTC market in recent years. 

Option Pricing
To make it simple, option premium consists of intrinsic value and time value. Out-of-the-money options consists merely time value and only in-the-money options contains intrinsic value. Intrinsic value is the price difference between the exercise price and the asset price at a specific point of time.

Premium = Intrinsic Value + Time Value

Option Pricing Model
Binomial and Black-Scholes are two most popular models calculating option premium. The Binomial model mainly assumes the price of the underlying asset will move up and down based on certain probabilities, with the prevailing stock price as latest option theoretical value. The original Black-Scholes model is used to calculate the pricing of European options (no dividends). By keying in information including the exercise price, underlying asset price, risk-free interest rate, days to maturity and volatility, the theoretical value of the option can be calculated.  

 Back to Top

Common Strategy - Single Strategy

1.	Long Call Options Buy Call Option with Exercise Price S
	Application Outlook on market is bullish and optimistic, call options with high exercise price (out-of-the-money) should be bought to achieve the highest leverage Breakeven Point S + Option Premium Paid Potential Gain Settlement price > Breakeven Point: Settlement Price - Breakeven Point Maximum Loss Limited to the Option Premium Paid
Back to Top
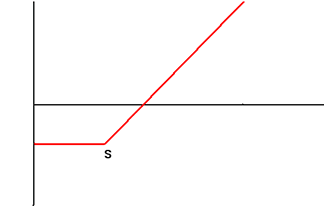
2	Short Call Options Sell Call Option with Exercise Price S
	Application Outlook is bearish, short call options to earn premium Breakeven Point S + Option Premium Received Potential Gain Settlement Price < Breakeven Point: Breakeven Point - Settlement Price Topped by Option Premium Received Maximum Loss Unlimited
Back to Top
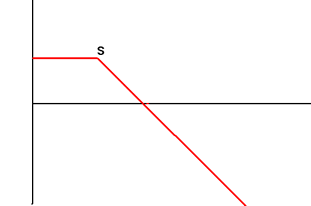
3	Long Put Options Buy Put Option with Exercise Price S
	Application Outlook is bearish, put options with low exercise price (out-of-the-money) should be bought to achieve the highest leverage Breakeven Point S - Option Premium Paid                     Potential Gain Settlement price < Breakeven Point: Breakeven Point - Settlement Price Maximum Loss Limited to the Option Premium Paid
Back to Top
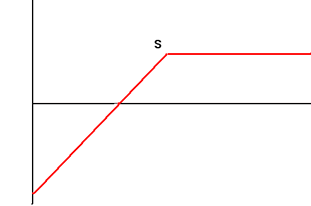
4.	Short Put Options Sell Put Option with Exercise Price S
	Application Outlook is optimistic, sell put options to receive options premium Breakeven Point S - Option Premium Received Potential Gain Settlement Price > Breakeven Point: Settlement Price - Breakeven Point Topped by the Option Premium Received Maximum Loss Exercise Price - Option Premium Received
Back to Top

Portfolio Strategy

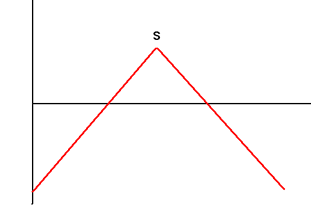
1.	Long Straddle  Buy Call and Put Options with Exercise Price S and Same Maturity
	Application Outlook on market is bullish and optimistic, call options with high exercise price (out-of-the-money) should be bought to achieve the highest leverage Breakeven Point S + option premium paid Potential Gain Settlement Price > Breakeven Point: Settlement Price - Breakeven Point Maximum Loss Limited by Option Premium Paid
Back to Top
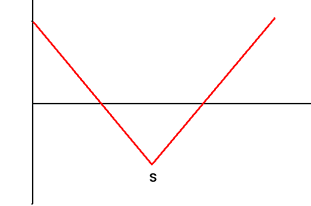
2	Short Straddle Sell Call and Put Options with Exercise Price S and Same Maturity
	Application Outlook: Reduction of market volatility Breakeven Point 1. Lower Breakeven Point: S - Option Premium Received   2. Higher Breakeven Point: S + Option Premium Received Potential Gain 1. Settlement Price < S: Settlement Price - Lower breakeven point     Topped by Option Premium Received   2. Settlement Price > S: Higher Breakeven Point - Settlement Price     Topped by Option Premium Received Maximum Loss 1. Settlement Price < Lower Breakeven Point: Lower Breakeven Point   2. Settlement Price > Higher Breakeven Point: Nil
Back to Top
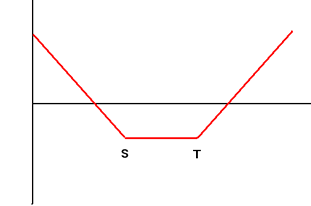
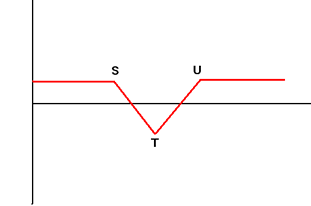
3	Long Strangle Buy Put Option with Exercise Price S and Call Option with Exercise Price T with the same maturity at the same time
	Application Outlook: Market will fluctuate significantly but direction is uncertain. Cost involved is lower than Long Straddle Breakeven Point 1. Lower Breakeven Point, S - Total amount of Option Premium Paid                          2. Higher Breakeven Point, T + Total amount of Option Premium Paid Potential Gain 1. Settlement Price < Lower Breakeven Point: Lower Breakeven Point - Settlement Price   2. Settlement Price > Higher Breakeven Point: Unlimited Maximum Loss Topped by Option Premium Paid
Back to Top
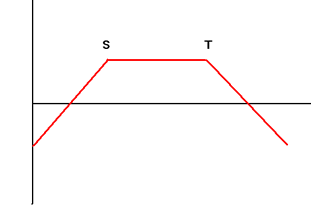
4.	Short Strangle Sell Put Option with Exercise Price S and Call Option with Exercise Price T with the same maturity simultaneously
	Application Outlook:: Market will fluctuate within a narrow range Breakeven Point 1. Lower Breakeven Point, S - Total amount of Option Premium Received      2. Higher Breakeven Point, T + Total amount of Option Premium Received    Potential Gain 1. Settlement Price < S: Settlement Price - Lower Breakeven Point   2. Settlement Price > T: Higher Breakeven Point - Settlement Price     3. T > Settlement Price > S: Total amount of Option Premium Received Maximum Loss 1. Settlement Price < Lower Breakeven Point: Lower Breakeven Point   2. Settlement Price > Higher Breakeven Point: Nil
Back to Top
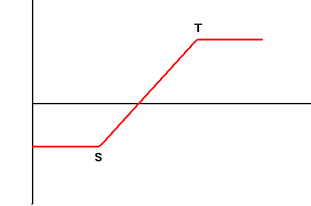
5.	Bullish Call Spread Buy Call Option with Exercise Price S and Sell Call Option with Exercise Price T with the same maturity simultaneously
	Application Outlook: Market will have a moderate upward trend and the cost involved is longer than buying a single call option Breakeven Point S + Net Option Premium Paid Potential Gain T - S - Net Option Premium Paid Maximum Loss Net Option Premium Paid
Back to Top
6.	Bullish Put Spread Buy Put Option with Exercise Price S and Sell Put Option with Exercise Price T with the same maturity simultaneously
	Application Outlook: Market will have a moderate upward trend Breakeven Point T - Net Option Premium Received Potential Gain Settlement Price - Breakeven Point Topped by Net Option Premium Received Maximum Loss T - S - Net Option Premium Received
Back to Top
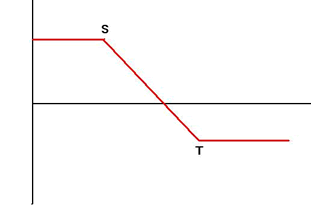
7.	Bearish Call Spread  Sell Call Option with Exercise Price S and Buy Call Option with Exercise Price T with the same maturity simultaneously
	Application Outlook: Market will have a moderate downward trend Breakeven Point S + Net Option Premium Received Potential Gain Breakeven Point - Settlement Price Topped by Net Option Premium Received Maximum Loss T - S - Net Option Premium Received
Back to Top
8.	Bearish Put Spread  Sell Put Option with Exercise Price S and Buy Put Option with Exercise Price T with the same maturity simultaneously
	Application Outlook: Market will have a moderate downward trend Breakeven Point T - Net Option Premium Paid Potential Gain Breakeven Point - Settlement Price, Topped by T - S - Net Option Premium Paid Maximum Loss Net Option Premium Paid
Back to Top
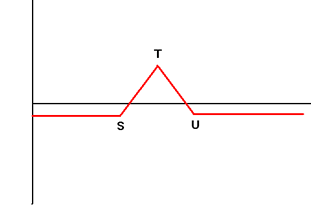
9.	Long Butterfly Buy Call (Put) Option with Exercise Price S, Sell 2 Call (Put) Options with Exercise Price T, Buy Call (Put) Option with Exercise Price U  Condition: T - S = U - T
	Application Outlook: Lower volatility in market Breakeven Point 1. Lower Breakeven Point: S + Net Option Premium Paid   2. Higher Breakeven Point: U - Net Option Premium Paid Potential Gain 1. T > Settlement Price > Lower Breakeven Point: Settlement Price - S - Net Option Premium Paid, Topped by T - Lower breakeven point   2. Higher Breakeven Point > Settlement Price > T: U - Settlement Price - Net Option Premium Paid       Topped by Higher Breakeven Point -  T Maximum Loss Limited to Net Option Premium Paid
Back to Top
10.	Short Butterfly Sell Call (Put) Option with Exercise Price S, Buy 2 Call (Put) Options with Exercise Price T, Sell Call (Put) Option with Exercise Price U  Condition: T - S = U - T
	Application Outlook: Higher volatility in market Breakeven Point 1. Lower Breakeven Point: S + Net Option Premium Received   2. Higher Breakeven Point: U - Net Option Premium Received Potential Gain 1. Settlement Price < Lower Breakeven Point: Lower Breakeven Point - Settlement Price     Topped by Net Option Premium Received   2. Settlement Price > Higher Breakeven Point: Settlement Price - Higher Breakeven Point     Topped by Net Option Premium Received Maximum Loss T - S - Net Option Premium Received or U - T - Net Option Premium Received

 Back to Top